问题
问答题
试确定常数a与b,使得经变换u=x+ay,υ=x+by,可将方程
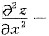
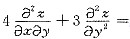 化为
化为
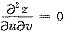 ,并求z=z(x+ay,x+by).
,并求z=z(x+ay,x+by).
答案
参考答案:z与x,y的脉络关系如图所示:[*],于是
[*]
代入所给方程,得
[*]
按题意,应取
1-4a+3a2=0, 1-4b+3b2=0.
即 (1-3a)(1-a)=0,(1-3b)(1-b)=0.
组合配对
[*]
若取第1对时,[*]的系数为0,与题目要求不符.同理,取第4对时,[*]的系数亦为0.只在取[*]或[*]时,有[*],从而知
[*]
其中ψ(υ)为υ的任意的可微函数.于是
z=∫ψ(υ)dυ+ψ(u)=Φ(υ)+ψ(u)
其中ψ(u)为u的任意的可微函数,Φ(υ)为ψ(υ)的一个原函数.取[*],b=1时,得
[*]
取a=1,[*]时,得
[*]
由于Φ与ψ的任意性,所以两组解其实是一样的.
