问题
问答题
设齐次线性方程组
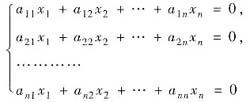
的系数矩阵A=(aij)n×n的秩为n-1,试证:此方程组的一般解(全部解)为

其中Aij(1≤j≤n)是aij的代数余子式,且至少有一个Aij≠0.
答案
参考答案:由r(A)=n-1<n,齐次线性方程组有非零解,其基础解系中含有一个解向量,并且A中至少存在一个n-1阶子式不等于零,不妨设Aij≠0(1≤i,j≤n).
根据行列式展开定理,有
[*]
而|A|=0,所以齐次方程组的一个基础解系为(Ai1,Ai2…,Ain)T;齐次方程组的全部解为x=c(Ai1,Ai2…,Ain)T,其中c为任意常数.
