问题
计算题
如图所示,水平地研上静止放置着物块B和C,相距l=1.0m物块A以速度v0=10m/s沿水平方向与B正碰碰撞后A和B牢固地粘在一起向右运动,并再与C发生正碰,碰后瞬间C的速度v=2.0m/s已知A和B的质量均为m,C的质量为A质量的k倍,物块与地面的动摩擦困数μ=0.45(设碰撞时间很短,g取10m/s2)
(1)计算与C碰撞前瞬间AB的速度;
(2)根据AB与C的碰撞过程分析k的取值范围,并讨论与C碰撞后AB的可能运动方向。

答案
解:(1)设物体A、B的质量分别为mA和mB,A与B发生完全非弹性碰撞后的共同速度为v1。
取向右为速度正方向,由动量守恒定律mAv0=(mA+mB)v1 ①
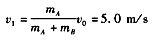
设AB运动到C时的速度为v2,由动能定理
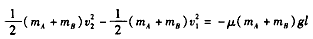 ②
②
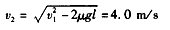
(2)设与C碰撞后AB的速度为v3,碰撞过程中动量守恒,有(mA+mB)v2=(mA+mB)v3+mCv ④
碰撞过程中,应有碰撞前的动能大于或等于碰撞后的动能,即
 ⑤
⑤
由④式,得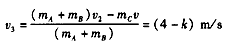 ⑥
⑥
联立⑤和⑥式,得k≤6 即:当k=6时,碰撞为弹性碰撞;
当k<6时,碰撞为非弹性碰撞。⑦
碰撞后AB向右运动的速度不能大于C的速度。
由⑥式,得 4 -k≤2k≥2
所以k的合理取值范围是6≥k≥2
综上得到: 当取k=4时,v3=0,即与C碰后AB静止 ⑧
当取4 >k≥2时,v3>0,即与C碰后AB继续向右运动⑨
当取6≥k>4时,v3<0,即碰后AB被反弹向左运动⑩
