问题
问答题
设α1=(1,-2,1,0,0)T,α2=(1,-2,0,1,0)T,α3=(0,0,1,-1,0)T,α4=(1,-2,3,-2,0)T是线性方程组
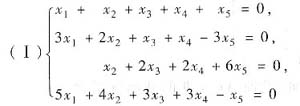
的解向量,问α1,α2,α3,α4是否构成方程组(Ⅰ)的基础解系,若能,说明理由,若不能,请增或减向量,使其成为基础解系.
答案
参考答案:将方程组(Ⅰ)的系数矩阵作初等行变换化成阶梯形矩阵,有
[*]
知r(A)=2,方程组中未知量个数是5,基础解系应由5-r(A)=3个线性无关解向量组成.将(α1,α2,α3,α4)作初等行变换化为阶梯形矩阵,有
[*]
r(α1,α2,α3,α4)=2,其中α1,α2(或α1,α3,或α1,α4)是极大线性无关组.
故α1,α2,α3,α4不构成方程组(Ⅰ)的基础解系,应去除与α1,α2线性相关的解向量α3,α4,增添一个与α1,α2线性无关的解向量.
因α1=(1,-2,1,0,0)T,α2=(1,-2,0,1,0)T,故将Ax=0的同解方程组
[*]
的自由未知量(x3,x4,x5)取成(0,0,1),代入方程解得β=(5,-6,0,0,1)T,则α1,α2,β是Ax=0的3个线性无关解向量,且满足n-r(A)=3,故α1,α2,β即是Ax=0的基础解系.
