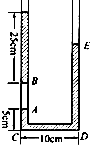
如图所示,截面均匀的U形玻璃细管两端都开口,玻璃管足够长,管内有两段水银柱封闭着一段空气柱,若气柱温度是27℃时,空气柱在U形管的左侧,A、B两点之间封闭着的空气柱长为15cm,U形管底边长CD=10cm,AC高为5cm.已知此时的大气压强为75cmHg.
(1)若保持气体的温度不变,从U形管左侧管口处缓慢地再注入25cm长的水银柱,则管内空气柱长度为多少?
某同学是这样解的:对AB部分气体,初态p1=100cmHg,V1=15Scm3,末态p2=125cmHg,V2=LScm3,则由玻意耳定律p1V1=p2V2解得管内空气柱长度L=12cm.以上解法是否正确,请作出判断并说明理由,如不正确则还须求出此时管内空气柱的实际长度为多少?
(2)为了使这段空气柱长度恢复到15cm,且回到A、B两点之间,可以向U形管中再注入一些水银,且改变气体的温度.问:应从哪一侧管口注入多长的水银柱?气体的温度变为多少?
(1)不正确.
因为ACE段水银柱总长只有45cm,所以在左侧缓慢加入25cm长水银柱后,左侧竖直管中只可能保留45cm长的水银柱.故末状态的压强不为125cmHg.
已知 p1=100cmHg,V1=15S,T1=300K;
p2=(75+45)cmHg=120 cmHg,V2=l2S
p1 V1=p2 V2
L2=12.5cm
(2)由水银柱的平衡条件可知向右侧注入25cm长的水银柱才能使空气柱回到A、B之间.
这时空气柱的压强为:
P3=(75+50)cmHg=125cmHg
由查理定律,有:
=P1 T1 P3 T3
解得T3=375K
答:(1)管内空气柱长度为12.5cm;
(2)应从右侧管口注入25cm的水银柱,气体的温度变为375K.
