问题
计算题
（16分）如图所示，一根内壁光滑的直角三角形玻璃管子处于竖直平面内，倾斜角为θ= 37°，让两个小球分别从顶点A由静止开始出发，一个球沿AC滑下，到达C所用的时间为t1，另一个球竖直自由下落经过B到达C，所用的时间为t2，在转弯处有个极小的光滑圆弧，可确保小球转弯时无机械能损失，且转弯时间可以忽略不计。问：
（1）计算t1∶ t2的值；
（2）若用同样的玻璃管把ABC轨道改为如图所示的ADEFC（在转弯处均有个极小的光滑圆弧），仍让小球从A静止开始运动，依次通过D、E、F后到达C点所用时间为t3，试定性说明t3和t1、t2的大小关系。
答案
解：(1)设内壁光滑的直角三角形玻璃管三边AB、BC、AC分别为3l、4l、5l，由AC边滑下，根据牛顿第二定律可得加速度a=gsinθ=6m/s2。
由5l=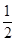
at12，解得t1=5
。
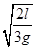沿ABC滑下，在AB段由3l=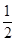gt212，解得t21=
。
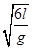沿水平段BC运动速度，v= gt21=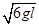
，
由4l=vt22，解得t22=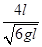
。
t2= t21 +t22=5。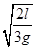
t1∶ t2=1 ∶ 1。
即两球同时释放同时到达。
（2）若用同样的玻璃管把ABC轨道改为如图所示的ADEFC，若球沿ADEF到C，则可判断小球在水中管中运动时间是相等的。沿DE运动时速度比在BC中运动时要小，故在水平管中运动时间长，所以沿ABC管运动时间比沿ADEFC的时间要短一些，所以t3> t2= t1.
应用牛顿第二定律和运动学公式列方程解答。