问题
填空题
设B是3阶非零矩阵,已知B的每一列向量都是方程组
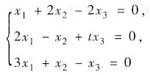
的解,则t=______时,矩阵B至多有_______列线性无关.
答案
参考答案:1,1
解析:
[分析]: 非零矩阵B的列向量是方程组的解,等价于齐次线性方程组有非零解.这是3个未知数3个方程的方程组,它有非零解则其系数矩阵A的行列式|A|=0,由此可解出参数t.求矩阵B至少有多少列线性无关,等价于求矩阵B的秩的上限.依题意,有AB=0,根据矩阵的秩的性质,有r(A)+r(B)≤n此时问题就转化为求矩阵A的秩.
记方程组的系数矩阵为
[*]
依题意方程组Ax=0有非零解,所以
[*]
解得t=1.
又依题意有AB=0,于是r(A)+r(B)≤3.
当t=1时,
[*]
显然,r(A)=2,故有r(B)≤1,所以B至多有1列线性无关.
