问题
计算题
（14分）如图所示，一固定在地面上的金属轨道ABC，AB与水平面间的夹角为α=37°，一小物块放在A处（可视为质点），小物块与轨道间的动摩擦因数均为μ=0.25，现在给小物块一个沿斜面向下的初速度v0=1m/s。小物块经过B处时无机械能损失，物块最后停在B点右侧1.8米处（sin37°=0.6，cos37°=0.8，g取10m/s2）。求：
（1）小物块在AB段向下运动时的加速度；
（2）小物块到达B处时的速度大小；
（3）求AB的长L。
答案
（1）4m/s2（2）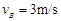
（3）1m
本题考查牛顿第二定律和动能定理，首先对小物块的受力，由牛顿第二定律可求出加速度大小，分析小物块的运动过程，由动能定理计算速度
（1）小物块从A到B过程中，由牛顿第二定律
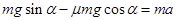
代入数据解得 a=4m/s2……………………………………………(5分)
（2）小物块从B向右运动，由动能定理
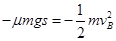
代入数据解得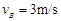…………………………………………..(5分)
（3）小物块从A到B，由运动学公式，有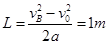
………………..(4分)