问题
问答题
设A，B是n阶矩阵．
(Ⅰ)A是什么矩阵时，若AB=A，必有B=E；
A是什么矩阵时，有B≠E，使得AB=A．
(Ⅱ)
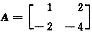，求所有的B≠E，使得AB=A．
答案
参考答案：(Ⅰ)当A是可逆阵时，若AB=A，两边左乘A-1，必有B=E；当A不可逆时，有B≠E，使得AB=A．因A不可逆时AX=0有非零解，设Aξi=0，i=1，2，…，n，合并得A[ξ1，ξ2，…，ξn]=0．令[ξ1，ξ2，…，ξn]=B-E，
则A(B-E)=0，得AB=A，其中B-E≠0，B≠E．
(Ⅱ)[*]有解[*]，即有
[*]，其中k，l是任意常数．
令[*]，得[*](k，l不同时为0，因A(B-E)=0，故有AB=A)．