问题
问答题
圆周角定理证明思路如下:
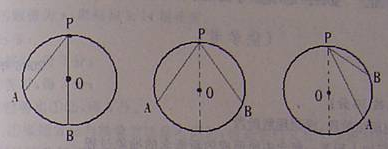
将圆周角的两边所处的位置分成三种情况:
①角的一边落在直径上;
②角的两边在某一直径的两铡;
③角的两边在某一直径的同侧。
如上图所示。先对情况①进行证明,然后将情况②、③转化为情况①分别进行证明。
最后得出圆周角定理对任意圆周角都成立的结论。
试具体分析上述证明中需要用到哪些数学思想方法。
答案
参考答案:
该证明中用到下面几种数学思想方法:
①将圆周角分成三朴情况,用到分类方法;
②先证明角恰有—边正直径上的特殊情况,用别特殊化方法。
③将其他两种情况转化为角恰有—边在直径上的情况,用到化归方法;
④通过对所有三种情况的证明.然后得出圆周角定理的结论,用到完全归纳法
⑤在证明过程巾需要进行演绎推理.因此用到演绎方法。
因为在《几何原本》中.除了推导时所需要的逻辑规则外,每个定理酌证明所采用的论据均是公设、公理或前面已经证明过酌定理.并且引入的概念(除原始概念)也基本上是符合逻辑上对概念下定义的要求.原则上不再依赖其它东西。围此《几何原本》是一个封闭的演绎体系。
另外,《几何原本》的理论体系回避任何与社会生产现实生活有关的应用问题,因此对于社会生活的各个领域来说,它也是封闭的。
