问题
问答题
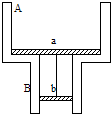
如图所示V的气缸是由横截面积不等的两段圆柱形竖直管道A和B相互连接而成,A的截面积SA=40cm2,B的截面积SB=20cm2,其中用光滑不漏气的活塞a和b封闭着一定量的理想气体,已知活塞a的质量ma=8kg,活塞b的质量mb=4kg,两活塞用一段不可伸长的细绳相连,最初活塞a位于管道A的下端,此时,气体的温度为-23°C,细绳恰好伸直但无张力,然后对气缸缓慢加热,使气体温度升高,已知大气压强p0=105Pa,求:
(1)开始时气体的压强p1;
(2)温度上升到多高时,两活塞开始上升;
(3)温度上升到多高时,活塞b才能上升到管道B的上端?
答案
(1)对活塞b分析,根据共点力平衡得,mbg+p1SB=p0SB,
解得:p1=p0-
=0.8×105Pa,mbg SB
(2)对a、b活塞分析,mag+mbg+p0SA+p2SB=p2SA+p0SB,
p2=p0+
=1.6×105Pa,(mag+mbg) SA-SB
根据等容变化得,
=p1 T1
,p2 T2
解得T2=500K.
(3)根据等压变化有:
=sb T2
,sa T3
解得T3=1000K
答:(1)开始时气体的压强为0.8×105Pa.
(2)温度上升到500K时,两活塞开始上升.
(3)温度上升到1000K时,活塞b才能上升到管道B的上端.
