问题
计算题
两个完全相同的物块A、B，质量均为m="0.8" kg，沿同一粗糙水平面以相同的初速度从同一位置运动。利用速度传感器可以在计算机上得到它们速度随时间的变化关系如图所示，图中的两条直线分别表示A物块受到水平拉力F作用和B物块不受拉力作用的v-t图象。求：
（1）物块A所受拉力F的大小。
（2）4 s末物块A、B之间的距离s。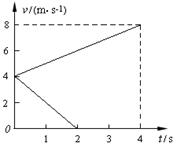
答案
（1）F="2.4" N（2）20 m
(1)设A、B两物块的加速度分别为a1、a2,
由v-t图可得
①
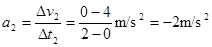，负号表示加速度方向与初速度方向相反。 ②
算出(a=2m/s2同样给分)
对A、B两物块分别由牛顿第二定律得
F－f=ma1 ③
f=ma2 ④
由①~④式可得 F="2.4" N ⑤
(2)设A、B两物块4 s内的位移分别为s1、s2，由图象得
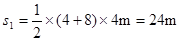⑥
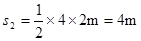⑦
所以 s=s1－s2="20" m ⑧
（用其它方法得出正确答案同样给分）
评分标准：本题13分. （1）问8分，①、②、③式各2分，、④、⑤式各1分；（2）问5分，⑥、⑦式各2分，⑧式1分
本题考查的是运动描述中V-T的应用，根据图中的信息可求出两个物体的加速度。根据牛顿第二定律可得两物体的受力大小，第二问中先算两物体在4s内的位移，即可得出4s时的间隔。