（18分）2010年10月1日18时59分57秒，我国成功地发射了“嫦娥二号”探月卫星。发射卫星的火箭长征三号丙全长54.84m，起飞时总质量M0=345t（吨）。发射的初始阶段，火箭竖直升空，仪器显示卫星对支持的平台最大压力达到卫星重的5倍。五天后，卫星经三次变轨后，进入圆形绕月工作轨道，绕月飞行周期118min。(地球表面的重力加速度g取10m/s2)。
（1）求发射的初始阶段（假设火箭总质量不变），火箭受到的最大推力；
（2）“嫦娥二号”探月卫星从远月点8000多公里变轨到100公里过程应加速还是减速？
（3）已知月球表面的重力加速度约为地球表面重力加速度的
，卫星做圆周运动的周期用T表示，月球半径用R表示。 请导出卫星圆轨道离月面高度的字母表达式。
（1）
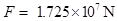（2）应减速。（3）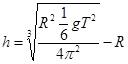
（1）设火箭发射初始阶段的最大加速度为a，卫星受到的最大支持力为N，卫星质量为m0，根据牛顿第二定律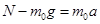 
…………………（2分）
依题意和牛顿第三定律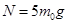
…………………………（2分）解得
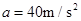………………………………………………………………（1分）设发射初始阶段火箭受到的最大推力为F，根据牛顿第二定律
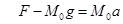………………………………………………………………（2分）解得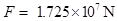………………………………………………………（1分）
（2）应减速。 ………………………………………… （3分）
（3）设月球质量为M, 卫星的质量为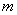
，距月面的高度为h，则卫星受到月球的引力为卫星提供向心力 
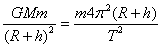………………（3分）月面物体所受万有引力近似等于重力，设物体质量为
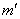，则
……………………………………………………………………（2分） 解得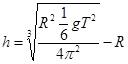：………………………………………………………（2分）
本题考查的是牛顿定律和万有引力定律的应用问题，首先根据牛顿定律解出加速度进而解出所受推力；根据引力提供向心力计算出卫星的轨道高度；