（14分）如图所示，足够长的传送带与水平面倾角θ=37°，以12米/秒的速率逆时针转动。在传送带底部有一质量m = 1.0kg的物体，物体与斜面间动摩擦因数μ= 0.25，现用轻细绳将物体由静止沿传送带向上拉动，拉力F = 10.0N，方向平行传送带向上。经时间t = 4.0s绳子突然断了，（设传送带足够长）求：
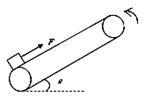
（1）绳断时物体的速度大小；
（2）绳断后物体还能上行多远；
（3）从绳断开始到物体再返回到传送带底端时的运动时间。 （g = 10m/s2，sin37°= 0.6，cos37°= 0.8，）
（1）8.0m/s (2) 4.0m(3)3.3s
（1）物体开始向上加速运动，受重力mg，摩擦力Ff，拉力F，设加速度为a1，
F – mgsinθ－ Ff = ma1
Ff = μFN
FN = mgcosθ
得a1 =" 2.0m" / s2 ‑‑‑‑‑‑‑‑（2分）
t = 4.0s时物体速度v1 =a1t =" 8.0m/s" ‑（1分）
(2) 绳断时,物体距传送带底端s1 =a1t 2 /2= 16m.
设绳断后 -mgsinθ- μmgcosθ= ma2
a2 =" -8.0m" / s2 ‑‑（2分）
t2 = -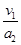
= 1.0s ‑‑（2分）
减速运动位移s2=v1t2+ a2t2 2 /2=4.0m‑‑（2分）
(3)物体加速下滑, mgsinθ＋ μmgcosθ= ma2
a3 =" 8.0m" / s2
当物体与传送带共速时向下运动距离s3=v2/(2a3)=9m‑（2分）
用时t3 =" v" / 3=1.5s‑‑‑‑‑‑（2分）
共速后摩擦力反向，由于mgsinθ 大于 μmgcosθ，物体继续加速下滑
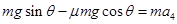
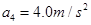
下滑到传送带底部的距离为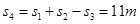
设下滑时间为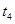
由
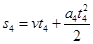得
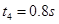
得：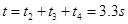
本题考查牛顿第二定律的应用，物体向上运动过程中由拉力重力沿斜面向下的分力和摩擦力提供加速度，由运动学公式可求得4s末的速度大小，绳子断后，物体沿传动带向上减速运动，由重力和摩擦力提供加速度，再由运动学公式求得运动时间，由位移和时间的关系求得位移大小