问题
计算题
（18分）如图所示，在倾角为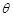
的光滑斜面上端系着一劲度系数为k的轻弹簧，弹簧的下端连有一质量为m的小球，球被一垂直于斜面的挡板A挡住，此时弹簧没有形变．若手持挡板A以加速度a（a < gsin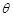）沿斜面向下做匀加速运动，求：
（1）从挡板开始运动到球与挡板分离所经历的时间；
（2）从挡板开始运动到小球的速度达到最大，球所经过的路程．
答案
(1) 
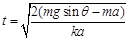(2) 
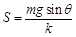
(1) 当球与刚挡板分离时，球与板有相同的加速度，但它们之间无相互作用。设此时小球的位移为x：
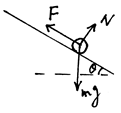
小球受力如图：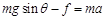
……（4分）
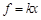…… （2分）
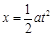…… （2分）
解得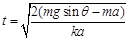： …… （1分）
(2) 挡板与球分开后，球先加速，后减速
当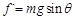
时，有最大速度 (4分)
此时，弹簧伸长量为x`，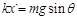
，即
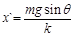（4分）
球经过的路程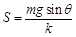 （1分）
本题考查牛顿第二定律的应用，当球与刚挡板分离时，球与板有相同的加速度，但它们之间无相互作用，根据此条件分析小球的受力情况，根据牛顿第二定律列公式求得加速度大小，再由位移与时间的关系求得运动时间，挡板与球分开后，球先加速，后减速，当重力沿斜面向下的分力等于摩擦力时小球的速度最大，由受力分析可求得此时弹簧的型变量，即为路程大小