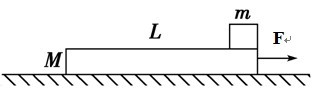
(12分)如图所示, 木板静止于水平地面上, 在其最右端放一可视为质点的木块. 已知木块的质量m＝1 kg, 木板的质量M＝4 kg, 长L＝2.5 m, 上表面光滑, 下表面与地面之间的动摩擦因数μ＝0.2.现用水平恒力F＝20 N拉木板, g取10 m/s2, 求:
(1)木板加速度的大小;
(2)要使木块能滑离木板, 水平恒力F作用的最短时间;
(3)如果其他条件不变, 假设木板的上表面也粗糙, 其上表面与木块之间的动摩擦因数为μ1＝0.3, 欲使木板能从木块的下方抽出, 需对木板施加的最小水平拉力;
(4)若木板的长度、木块质量、木板的上表面与木块之间的动摩擦因数、木板与地面间的动摩擦因数都不变, 只将水平恒力增加为30 N, 则木块滑离木板需要多长时间？
(1)2.5 m/s2 (2)1 s (3)25 N (4)2 s
(1)木板受到的摩擦力Ff＝μ(M＋m)g＝10 N
木板的加速度a＝
＝2.5 m/s2.
(2)设拉力F作用t时间后撤去
木板的加速度为a′＝－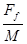
＝－2.5 m/s2
木板先做匀加速运动, 后做匀减速运动, 且a＝－a′, 故at2＝L
解得t＝1 s, 即F作用的最短时间为1 s.
(3)设木块的最大加速度为a木块, 木板的最大加速度为a木板, 则μ1mg＝ma木块
得: a木块＝μ1g＝3 m/s2
对木板: F1－μ1mg－μ(M＋m)g＝Ma木板
木板能从木块的下方抽出的条件: a木板>a木块
解得: F1>25 N.
(4)木块的加速度a木块＝μ1g＝3 m/s2
木板的加速度a木板＝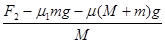
＝4.25 m/s2
木块滑离木板时, 两者的位移关系为s木板－s木块＝L, 即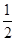
a木板t2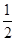－a木块t2＝L
代入数据解得: t＝2 s.
本题考查牛顿第二定律的应用，以木板为研究对象，木板向右运动过程中受到水平向右的拉力和摩擦力的作用，由牛顿第二定律可求得加速度大小，拉力F作用时间最短，是指当有拉力F时滑块向右匀加速运动，撤去拉力F后木板向右做匀减速直线运动，而木块向右一直在摩擦力作用下向右做匀加速直线运动，分阶段进行受力分析求得加速度，再由相对位移为木板的长度，可求得拉力F的临界值