问题
计算题
如图,用绳AC和BC吊起一重物,绳与竖直方向夹角分别为30°和60°,AC绳能承受的最大的拉力为150N,而BC绳能承受的最大的拉力为100N,求物体最大重力不能超过多少?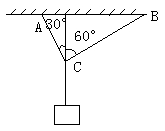
答案
不能超过173.2N
【错解分析】错解:以重物为研究对象,重物受力如图2-13。由于重物静止,则有
TACsin30°=TBCsin60°
TACcos30°+TBCcos60°=G
将TAC=150N,TBC=100N代入式解得G=200N。
以上错解的原因是学生错误地认为当TAC=150N时,TBC=100N,而没有认真分析力之间的关系。实际当TBC=100N时,TBC已经超过150N。
【正解】以重物为研究对象。重物受力如图2-13,
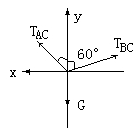
重物静止,加速度为零。据牛顿第二定律列方程
TACsin30°-TBCsin60°=" 0" ①
TACcos30°+TBCcos60°-G =" 0" ②
由式①可知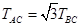 当
当 时,
时,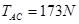 ,AC将断
,AC将断
而当TAC=150N时,TBC=86.6<100N
将TAC=150N,TBC=86.6N代入式②解得G=173.32N。
所以重物的最大重力不能超过173.2N。
