问题
计算题
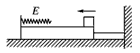
如图所示,质量为M上下表面光滑的长木板放在水平面上静止,右端用细线拴在竖直墙上,左端固定有一根轻弹簧。质量为m的小铁块以初速度v0从木板右端向左滑上木板,并压缩弹簧。当小铁块的速度减小为初速度的一半时,弹簧的弹性势能为E,此时细线刚好被拉断。求:为使木板能获得最大动能,M与m的比值应该是多大?(不计任何摩擦)
答案
解:设小铁块初速度为v0,则:
由能量守恒定律得E= mv02-
mv02-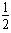 m·
m· v02=
v02=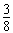 mv02
mv02
要使木板能获得最大动能,则弹簧恢复原长时,铁块速度为0
由动量守恒和能量关系得:m×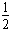 v0=Mv1,
v0=Mv1,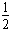 Mv12=
Mv12=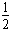 m×
m×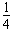 v02+E
v02+E
可得: