问题
计算题
(16分) 如图所示,长度L="1" m、质量M="0.25" kg的木板放在光滑水平面上,质量m="2" kg的小物块(可视为质点)位于木板的左端,木板和物块间的动摩擦因数μ=0.1.现突然给木板一向左的初速度v0="2" m/s,同时对小物块施加一水平向右的恒定拉力F="10" N,经过一段时间后,物块与木板相对静止,此时撤去拉力F，取g="10" m/s2,
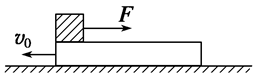
求:(1)物块最终停止在木板上的位置.
(2)上述过程中拉力F做的功.
答案
(1)0.5m (2)5J
题目分析：木块与木板间滑动摩擦力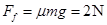
据牛顿第二定律知，木块的加速度为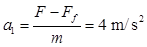
------2分
木板的加速度为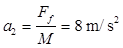
------2分
当木块、木板具有共同速度时，两者不再发生相对滑动，一直匀速运动下去.
所以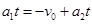
解得t="0.5" s ------3分
两者速度大小为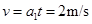
可见木板此时恰好回到原位置，位移为零 ------3分
此过程木块的位移为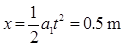
所以木块最终停在木板的中点上. ----2分
(2)拉力F做的功为W=Fx=5J ------4分
点评：难题。解决本题时要注意运动过程的分析，整个运动过程分物体、分阶段分析，问题就比较清晰，然后再逐段求解。