问题
计算题
（12分）如图所示，在水平向左匀强电场中，有一光滑半圆绝缘轨道竖直放置，轨道与一水平绝缘轨道MN连接，半圆轨道所在竖直平面与电场线平行，其半径R = 40cm。一带正电荷的小滑块质量为m =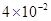
kg，已知小滑块所受电场力
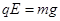，且与水平轨道间的摩擦可忽略，取g = 10m/s2，求：
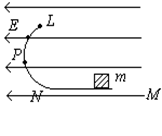
（1）要小滑块恰能运动到圆轨道的最高点L，滑块应在水平轨道上离N点多远处释放？
（2）这样释放的滑块通过P点时对轨道压力是多大？（P为半圆轨道中点）
答案
（1）S＝1m（2）2.4N
题目分析：（1）滑块刚能通过轨道最高点条件是 
(3分)
滑块由释放点到最高点过程由动能定理： 
(2分)
代入数据得：S＝1m (1分)
（2）滑块过P点时，由动能定理：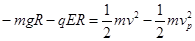 
(2分)
在P点由牛顿第二定律：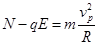 
(2分)
代入数据得：N＝2.4N (1分)
根据牛顿第三定律可知，轨道受到压力大小2.4N (1分)
点评：难度中等，明确最高点的速度不为零，在最高点时应有重力提供向心力，利用动能定理求解问题时只需注意初末位置，对运动过程可一带而过