问题
计算题
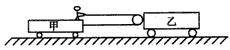
光滑水平地面上停放着甲、乙两辆相同的平板车，一根轻绳跨过乙车的定滑轮（不计定滑轮的质量和摩擦），绳的一端与甲车相连，另一端被甲车上的人拉在手中，已知每辆车和人的质量均为30 kg，两车间的距离足够远，现在人用力拉绳，两车开始相向运动，人与甲车保持相对静止，当乙车的速度为0.5 m/s 时，停止拉绳。求：
（1）人在拉绳过程做了多少功？
（2）若人停止拉绳后，至少以多大速度立即从甲车跳到乙车才能使两车不发生碰撞？
答案
解：（1）设甲、乙两车和人的质量分别为m甲，m乙和m人，停止拉绳时甲车的速度为v甲，乙车的速度为v乙，由动量守恒定律得
(m甲+m人)v甲=m乙v乙
求得v甲=0.25 m/s
由功与能的关系可知，人拉绳过程做的功等于系统动能的增加量
W=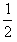
(m甲+m人)v甲2+
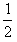m乙v乙2=5.625 J
（2）设人跳离甲车时人的速度为v人，人离开甲车前后由动量守恒定律得
(m甲+m人)v甲=m甲v甲'+m人v人
人跳到乙车时：m人v人-m乙v乙=(m人+m乙)v'乙
v'甲=v'乙
代入得：v人=0.5 m/s
当人跳离甲车的速度大于或等于0.5 m/s时，两车才不会相撞