问题
计算题
如图所示，水平传送带AB长l＝8.3 m，质量为M＝1 kg的木块随传送带一起以v1＝2 m/s的速度向左匀速运动(传送带的传送速度恒定)，木块与传送带间的动摩擦因数μ＝0.5.当木块运动至最左端A点时，一颗质量为m＝20 g的子弹以v0＝300 m/s水平向右的速度正对射入木块并穿出，穿出速度v＝50 m/s，以后每隔1 s就有一颗子弹射中木块，设子弹射穿木块的时间极短，且每次射入点各不相同，g取10 m/s2.求：
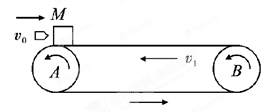
(1)第一颗子弹射入木块并穿出时木块的速度；
(2)在被第二颗子弹击中前，木块向右运动离A点的最大距离．
答案
(1)3 m/s (2)0.9 m
【正解】(1)设子弹第一次射穿木块后木块的速度为v′(方向向右)，则在第一次射穿木块的过程中：
对木块和子弹整体由动量守恒定律(取向右为正方向)得
mv0－Mv1＝mv＋Mv′
解得v′＝3 m/s，方向向右．
(2)木块向右滑动中加速度大小为a＝μg＝5 m/s2，以速度v′＝3 m/s向右滑行，速度减为零时所用时间为t1＝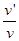
＝0.6 s
显然这之前第二颗子弹仍未射出，所以木块向右运动离A点的最大距离sm＝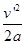
＝0.9 m.
【点评】此题考查了动量守恒定律、牛顿运动定律和运动学的基本规律在传送带问题中的应用情况，解答此题的关键是要求学生分析物理过程，建立清晰的物理情景，并注意到过程之间的内在联系．
