（12分）如图甲所示，一竖直面内的轨道是由粗糙斜面AB和光滑圆轨道BCD组成，AB与BCD相切于B点，C为圆轨道的最低点。将小物块（可看作质点）置于轨道ABC上离地面高为H处由静止下滑，可用力传感器测出其经过C点时对轨道的压力FN。现将小物块放在ABC上不同高度处，让H从零开始逐渐增大，传感器测出小物块每次从不同高度处下滑到C点时对轨道的压力FN，得到如图乙两段直线PQ和QI，且IQ反向延长线与纵轴交点坐标值为5 N，g取10 m/s2。
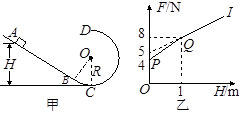
则
（1）小物块的质量m为多少？
（2）若小物块由斜面上某点从静止开始运动，恰好能通过圆轨道最高点D，求小物块在C点对轨道的压力FN大小为多少？
（3）小物块在斜面上某点由静止开始运动，并能通过C点。某同学根据图象所给信息求出圆轨道半径R=2m，轨道BC部分所对应的圆心角为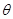
=60°。请你再结合图象所给的信息求出斜面对小物体的滑动摩擦力大小为多少？
(1) m =" 0.4" kg (2) 24 N (3)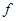
= 
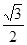N
题目分析：（1）由图像可知，当H = 0时 FN =" 4.0" N
FN = mg m =" 0.4" kg (2分，方程1分，结果1分)
（2）在D点由牛顿第二定律：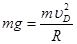
．．．．．．．．1分
C到D动能定理：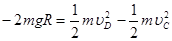
．．．．．．．．2分
在C点由牛顿第二定律：FN— mg =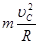
．．．．．．．．１分
FN =" 24" N．．．．．．．．１分
（3）在C点由牛顿第二定律：FN— mg =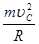
．．．．．．．．１分
由动能定理：mgH— 
= 
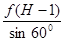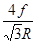．．．．．．．．１分
FN =" (2mg" —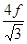 
)
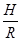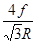++mg ．．．．．．．．１分
解法1：图像QI段斜率：k = (2mg— )
= 
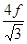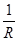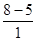= 3．．．．．．．．１分
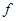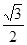= N．．．．．．．．１分
解法2：根据QI线与纵轴的截距：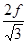 
+mg =" 5" ．．．．．．．．１分
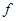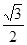= N．．．．．．．．１分
点评：本题关键是对分析清楚滑块的各个运动过程，然后运用动能定理、机械能守恒定律和向心力公式，结合图象联立方程组求解．