如图所示,水平面上固定着一个半径R=0.4m的 光滑环形轨道,在轨道内放入质量分别是M=0.2kg和m=0.1kg的小球A和 B(均可看成质点),两球间夹一短弹簧。
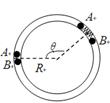
(1)开始时两球将弹簧压缩(弹簧的长度相对环形轨道半径和周长而言可忽略不计),弹簧弹开后不动,两球沿轨道反向运动一段时间后又相遇,在此过程中,A球转过的角度θ是多少?
(2)如果压缩弹簧在松手前的弹性势能E=1.2J,弹开后小球B在运动过程中受到光滑环轨道的水平侧压力是多大?
(1)θ=120°(2)4N
(1)在弹簧弹开的过程中系统动量守恒,假设A运动的方向为正方向,则
Mv1-mv2=0 2分
设从弹开到相遇所需时间为t,则有:
v1t+v2t=2πR 2分
联立以上两式得: 
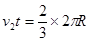 2分
2分
所以A球转过的角度为θ=120° 2分
(2)以A、B及弹簧组成的系统为研究对象,在弹簧张开的过程中,系统机械能守恒,则有  2分
2分
Mv1-mv2=0 2分
解得: v1=2m/s,v2=4m/s 2分
所以,小球B在运动过程中受到光滑轨道的侧压力是其所需向心力,即:
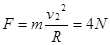 2分
2分
题目分析:
点评:做本题的关键是对各个过程中小球的动量,机械能是否守恒的判断