问题
单项选择题
下列结论中正确的是()。
A.如果矩阵A中所有顺序主子式都小于零,则A一定为负定矩阵
B.设A=(aij)m×n,若aij=aij,且aij>0(i,j=1,2…,n),则A一定为正定矩阵
C.如果二次型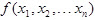 中缺少平方项,则它一定不是正定二次型
中缺少平方项,则它一定不是正定二次型
D.二次型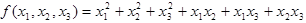 所对应的矩阵是
所对应的矩阵是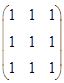
答案
参考答案:C
解析:
由惯性定理可知,实二次型 =xTAx经可逆线性变换化为标准型时,其标准型中正、负平方项的个数是唯一确定的。对于缺少平方项的n元二次型的标准形或规范形中正惯性指数不会等于未知数的个数n,所以一定不是正定二次型。A项,对称矩阵A为负定的充分必要条件是:奇数阶主子式为负,而偶数阶主子式为正。B项,对称矩阵A为正定的充分必要条件是:A的各阶主子式都为正。对于满足题干要求的矩阵
=xTAx经可逆线性变换化为标准型时,其标准型中正、负平方项的个数是唯一确定的。对于缺少平方项的n元二次型的标准形或规范形中正惯性指数不会等于未知数的个数n,所以一定不是正定二次型。A项,对称矩阵A为负定的充分必要条件是:奇数阶主子式为负,而偶数阶主子式为正。B项,对称矩阵A为正定的充分必要条件是:A的各阶主子式都为正。对于满足题干要求的矩阵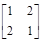 ,其2阶主子式为负,故其不是正定矩阵。D项,二次型
,其2阶主子式为负,故其不是正定矩阵。D项,二次型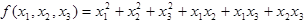 所对应的矩阵为
所对应的矩阵为 。
。
