问题
计算题
如图所示,长为R的不可伸长轻绳上端固定在O点,下端连接一小球,小球与地面间的距离可以忽略(但小球不受地面支持力)且处于静止状态.在最低点给小球一沿水平方向的初速度,此时绳子恰好没断,小球在竖直平面内做圆周运动。假设小球到达最高点时由于绳子碰到正下方P处的钉子恰好断裂,最后小球落在距初始位置水平距离为4R的地面上,重力加速度为g.试求:
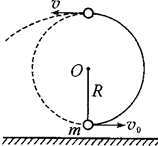
(1)绳突然断开时小球的速度v;
(2)竖直方向上O与P的距离L.
答案
(1)2(2)R/2
题目分析:小球飞出后做平抛运动,可求出速度大小,根据最高点、最低点合外力提供向心力可求解
(1)2R=(1/2)gt2
V t="4R"
得到v=2
(2) 最低点: F'向="T-mg=(mv02)/R"
得到绳子承受的最大力为 T=7mg
最高点:F向=T+mg=(mv2)/R'
得到 R'=R/2即P到O的距离L=R/2
点评:本题是平抛运动和圆周运动相结合的典型题目,除了运用平抛运动和圆周运动的基本公式外,求速度的问题,动能定理不失为一种好的方法.
