问题
计算题
如图所示,半径R=0.4m的光滑半圆轨道处于竖直平面内,半圆环与粗糙的水平地面切于圆环的端点A,一质量m=0.1kg的小球,以初速度v0=8.0m/s,从C点起在水平地面上向左运动,经A点冲上半圆轨道恰好通过轨道最高点B后水平抛出,取重力加速度g=10m/s2,求:
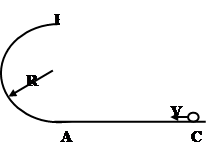
(1)小球在轨道B点时速度大小;
(2)小球从B点飞出到落回地面时的水平距离;
(3)小球从C点起经水平面到A时,克服摩擦力所做的功。
答案
(1)2m/s(2)0.8m(3)2.2J
题目分析:(1)小球做圆周运动恰好通过圆周轨道最高点B,重力提供向心力,
mg=mv2/R
VB= 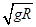 =2m/s
=2m/s
(2)小球从B点飞出做平抛运动,运动时间为t,则2R=gt2/2,可得t= 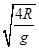 =0.4s
=0.4s
平抛水平距离为x=vBt=0.8m
(3)小球从A点冲向半圆轨道B,机械能守恒,mv2A/2=2mgR+mv2B/2
小球从C点经水平面到A点时,由动能定理有-Wf= mv2A/2- mv20/2
得wf= mv2o/2-(2mgR+ mv2B/2)=2.2J
