问题
计算题
一质量m=0.6kg的物体以v0=20m/s的初速度从倾角为30°的斜坡底端沿斜坡向上运动。当物体向上滑到某一位置时,其动能减少了ΔEk=18J,机械能减少了ΔE=3J,不计空气阻力,重力加速度g=10m/s2,求:
(1)物体向上运动时加速度的大小;
(2)物体返回斜坡底端时的动能。
答案
(1)6m/s2 (2)80J
(1)设物体在运动过程中所受的摩擦力大小为f,向上运动的加速度大小为a,由牛顿第二定律有
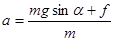
设物体动能减少ΔEk时,在斜坡上运动的距离为s,由功能关系得ΔEk=(mgsinα+f)s,ΔE=fs
联立以上各式并代入数据可得a=6m/s2。
(2)设物体沿斜坡向上运动的最大距离为sm,由运动学规律可得,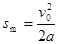
设物体返回底端时的动能为Ek,由动能定理有Ek=(mgsinα-f)sm
联立以上各式并代入数据可得,Ek=80J。
【考点定位】考查牛顿运动定律及动能定理。
