问题
计算题
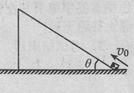
如图所示，质量m=0.2kg的小滑块从固定的粗糙斜面底端以平行于斜面的速度v0=18m/s滑上斜面。已知斜面倾角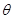
=37˚，小滑块与斜面间的动摩擦因数u=0.15，斜面足够长，重力加速度g=10m/s2，sin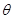=0.6，cos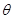=0.8求：
（1）小滑块向上滑动的时间t是多少？
（2）小滑块上滑的最大高度h是多大？
（3）小搰块从底端出发到回到底端的过程中，减少的机械能ΔE是多少？
答案
2.5 s 13.5m 10.8 J
题目分析：（1）设小滑块上滑的加速度大小是a1，则
ma1=mgsinθ＋μmgcosθ
v0=a1t
解得a1="7.2" m/s2，t =2.5s
（2）小滑块从斜面底端上滑到最高处的过程中，设沿斜面上滑的距离是x，根据动能定理有
－mgh－μmgxcosθ=0－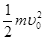
h= xsinθ
解得h=13.5m
另解：2a1x=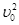
h= xsinθ
解得h=13.5m
（3）根据功能关系有△E=2μmgxcosθ
解得△E = 10.8J