问题
计算题
如图所示，在竖直面内有一光滑水平直轨道与半径为R＝0.25m的光滑半圆形轨道在半圆的一个端点B相切，半圆轨道的另一端点为C。在直轨道上距B为x(m)的A点，有一可看做质点、质量为m＝0.1kg的小物块处于静止状态。现用水平恒力将小物块推到B处后撤去恒力，小物块沿半圆轨道运动到C处后，恰好落回到水平面上的A点，取g＝10m/s2。求
（1）水平恒力对小物块做功W与x的关系式
（2）水平恒力做功的最小值
（3）水平恒力的最小值
答案
题目分析：小物块从C运动到A的运动是平抛运动。
设小球在C处的速度为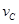
，
则由C到A
，
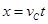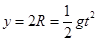
整理得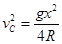
小球从A到C有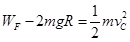
解得：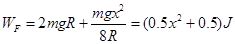
（2）当WF最小时，物块刚好能够通过C点，此时mvC2/R＝/mg
由C到A仍做平抛运动，所以vC2＝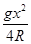
仍成立
由以上两式：x＝2R
代入公式可求得恒力做功的最小值为
WFmin＝（0.5＋0.5×4×0.252）J＝0.625J
（3）由功的公式得F＝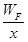
将WF＝（0.5x2＋0.5）J 代入上式得F＝（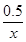
＋0.5x）N
由数学知识可知，当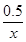＝0.5x，即x＝1时F最小 Fmin＝1N