问题
计算题
(14分)如图所示,在粗糙水平面上有一质量为M、高为h的斜面体,斜面体的左侧有一固定障碍物Q,斜面体的左端与障碍物的距离为d。将一质量为m的小物块置于斜面体的顶端,小物块恰好能在斜面体上与斜面体一起保持静止;现给斜面体施加一个水平向左的推力,使斜面体和小物块一起向左匀加速运动,当斜面体到达障碍物与其碰撞后,斜面体立即停止,小物块水平抛出,最后落在障碍物的左侧p处(图中未画出),已知斜面体与地面间的动摩擦因数为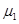 ,斜面倾角为
,斜面倾角为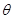 ,重力加速度为g,滑动摩擦力等于最大静摩擦力,求:
,重力加速度为g,滑动摩擦力等于最大静摩擦力,求:

(1)小物块与斜面间的动摩擦因数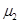 ;
;
(2)要使物块在地面上的落点p距障碍物Q最远,水平推力F为多大;
(3)小物块在地面上的落点p距障碍物Q的最远距离。
答案
见解析
题目分析:(1)物块恰好静止在斜面上: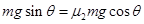
解得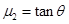
(2)要使物块距P点最远,应使物块随斜面体到Q点的速度最大,需要加速度最大
对物块受力分析可得: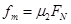 ①
①
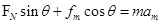 ②
②
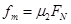 ③
③
由以上三式可解得 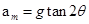
对整体列式: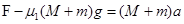
解得: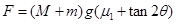
(3)物块抛出的速度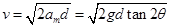
由平抛规律: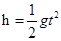 x=vt
x=vt
可解得: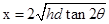
所以P距Q的距离为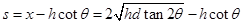 。
。
