问题
计算题
如图（1）所示，圆柱形气缸的上部有小挡板，可以阻止活塞滑离气缸，气缸内部的高度为d，质量不计的薄活塞将一定质量的气体封闭在气缸内。开始时活塞离底部高度为
，温度为t1=27℃，外界大气压强为p0=1.0×l05Pa，现对气体缓缓加热。求：
（1）气体温度升高到t2=127℃时，活塞离底部的高度；
（2）气体温度升高到t3=387℃时，缸内气体的压强；
（3）在图（2）中画出气体从27℃升高到387℃过程的压强和温度的关系图线。
答案
（1）
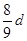；（2）1.467×105Pa；（3）见解析。
(10分)（1）假设气体温度达到tc时，活塞恰好移动到挡板处，气体做等压变化，设气缸横截面积为S，由盖·吕萨克定律得到：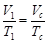
，即
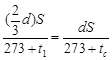（1分）
解出tc=
=177℃ （1分）
因为t2小于tc，所以温度升高到127℃前，气体做等压变化，设活塞离底部的高度为h，
由盖·吕萨克定律得到：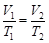
，即 （1分）
解出h=
（1分）
（2）当气体温度高于tc后，活塞受到挡板的阻碍，气体体积不再发生变化，（1分）
由查理定律得到：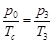
，即
， （1分）
解得
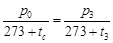（1分）
（3）三个状态的描点正确 （t1=27℃，p1=1×l05Pa；tc=177℃，pc=1×l05Pa；t3=387℃，p3=1.467×l05Pa）
（1分）
两段均为直线（未用直尺画的不得分） （1分）
标明过程（没有箭号不得分） （1分）