(10分)如图所示,光滑水平面上静止放置着一辆平板车A。车上有两个小滑块B和C(都可视为质点),B与车板之间的动摩擦因数为μ,而C与车板之间的动摩擦因数为2μ,开始时B、C分别从车板的左、右两端同时以大小相同的初速度v0相向滑行。经过一段时间,C、A的速度达到相等,此时C和B恰好发生碰撞。已知C和B发生碰撞时两者的速度立刻互换,A、B、C三者的质量都相等,重力加速度为g。设最大静摩擦力大小等于滑动摩擦力。 求:

(1)开始运动到C、A的速度达到相等时的时间t;
(2)平板车平板总长度L;
(3)若滑块C最后没有脱离平板车,求滑块C最后与车相对静止时处于平板上的位置。
(1)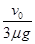 ,(2)
,(2)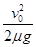 ;(3)滑块C最后停在车板右端
;(3)滑块C最后停在车板右端
题目分析:(1)设A、B、C三者的质量都为m,从开始到C、A的速度达到相等这一过程所需的时间为t,对C由牛顿运动定律和运动学规律有: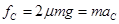 ,
,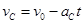
对A由牛顿运动定律和运动学规律有: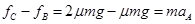
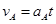 ,
,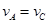
联立以上各式解得: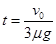
(2)对C,在上述时间t内的位移: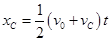
对B,由牛顿运动定律和运动学规律有: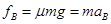 ,
, ,
,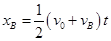
C和B恰好发生碰撞,有: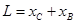
解得: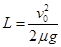
(3)对A,在上述时间t内的位移:
将t代入以上各式可得A、B、C三者的位移和末速度分别为:
 (向左),
(向左), (向右),
(向右),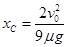 (向左)
(向左)
 (向左),
(向左),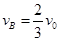 (向右)
(向右)
所以:C相对A向左滑动的距离: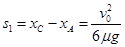
骣B发生碰撞时两都速度立即互换、则碰后C、B的速度各为:
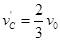 (向右),
(向右),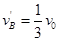 (向左)
(向左)
碰后B和A的速度相等。由分析可知,碰后B和A恰好不发生相对滑动,即保持相对静止一起运动。设C最后停在车板上时,共同速度为vt,由A、B、C组成的系统动量守恒可知:
 解得:vt=0
解得:vt=0
这一过程中,设C相对于A向右滑行的距离为S2,由能量关系可知:
 解得:
解得: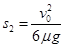
所以:滑块C恰好回到原来的位置,即滑块C最后停在车板右端。
