问题
计算题
(16分)如图所示,半径为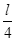 、质量为m的小球用两根不可伸长的轻绳a、b连接,两轻绳的另一端系在一根竖直杆的A、B两点上,A、 B两点相距为l,当两轻绳伸直后,A、B两点到球心的距离均为l。当竖直杆以自己为轴转动并达到稳定时(细绳a、b与杆在同一竖直平面内)。求:
、质量为m的小球用两根不可伸长的轻绳a、b连接,两轻绳的另一端系在一根竖直杆的A、B两点上,A、 B两点相距为l,当两轻绳伸直后,A、B两点到球心的距离均为l。当竖直杆以自己为轴转动并达到稳定时(细绳a、b与杆在同一竖直平面内)。求:

(1)竖直杆角速度ω为多大时,小球恰离开竖直杆?
(2)轻绳a的张力Fa与竖直杆转动的角速度ω之间的关系。
答案
(1) 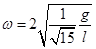
(2) ①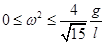 时,
时,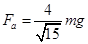 ②
②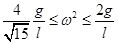 时,
时,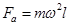 ③
③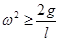 时,
时,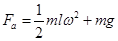
题目分析:(1)小球恰好离开竖直杆时,小球与竖直杆间的作用力为零,此时轻绳a与竖直杆间的夹角为α,由题意可知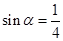
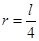 (1分)
(1分)
沿半径: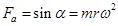 (1分) 垂直半径:
(1分) 垂直半径: (1分)
(1分)
联立解得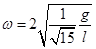 (1分)
(1分)
(2)由(1)可知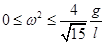 时,
时,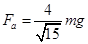 (2分)
(2分)
若角速度再增大,小球将离开竖直杆,在轻绳b恰好伸直前,设轻绳与竖直杆的夹角为β,此时小球做圆周运动的半径为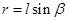 (1分) 沿半径:
(1分) 沿半径: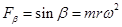 (1分) 垂直半径:
(1分) 垂直半径: (1分)
(1分)
联立解得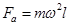 (1分)
(1分)
当轻绳恰好伸直时,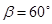 ,此时
,此时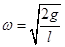 (1分)
(1分)
故有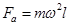 ,此时
,此时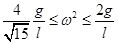 (1分)
(1分)
若角速度再增大,轻绳b拉直后,小球做圆周运动的半径为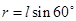 (1分)
(1分)
沿半径: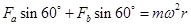 (1分)
(1分)
垂直半径: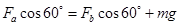 (1分)
(1分)
联立解得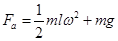 ,此时
,此时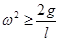 (1分)
(1分)
