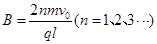问题
计算题
（19分）如图所示，在光滑绝缘的水平面上，固定一绝缘的、边长为
的正方形方框，方框内有大小可调、方向竖直向下的匀强磁场，方框左边界的中点有一小孔，恰能让质量为m、带电量为+q的小球b（可视为质点）无阻碍的通过。初始时，小球b静止在小孔处。边界线MN的左侧有一范围足够大的匀强电场区域，电场的电场强度为E，方向水平向左，MN的右侧与方框的左侧间的距离可忽略不计。现有另一质量为
、不带电的小球a以速度
正对b球运动。设所有的碰撞均无能量损失和电量的转移，不计一切摩擦，则：
（1）求小球a、b首次碰后的速度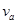
、
；
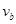（2）调节方框内磁场的磁感应强度的大小，使小球b与方框经过最少次数的碰撞后，从小孔离开。求小球a、b从开始相碰到再次相碰所用的时间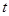
；
（3）方框内磁场的磁感应强度满足什么条件时，可使小球b绕方框中心运动一周后离开磁场。
答案
（1）
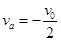，方向向左；
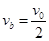，方向向右（2）
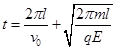（3）
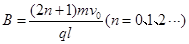或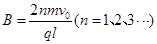
题目分析：（1）a与b发生弹性碰撞，满足动量守恒和机械能守恒，有：
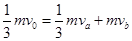
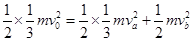
联立解得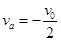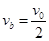：，，碰后a的速度方向向左，b的速度方向向右。
（2）当小球b做圆周运动的半径为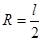
时，与方框碰撞3次后从小孔离开。
由：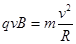
，得：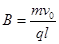
小球b在磁场中运动的时间为：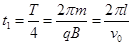
小球b离开磁场后经时间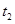
追上小球a，则：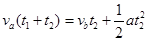
而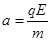 
解得：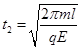
则a与b从开始相碰到再次相碰所用的时间为：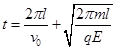
（3）当小球b做圆周运动的半径满足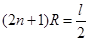
时可离开磁场，此时有：
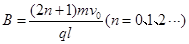
当小球做圆周运动的半径满足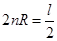
时可离开磁场，此时有：