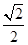问题
计算题
(16分)如图所示，ABDO是处于竖直平面内的光滑轨道，AB是半径R＝15m的四分之一圆周轨道，半径OA处于水平位置，BDO是直径为15m的半圆轨道，D为BDO轨道的中央，一个小球P从A点的正上方距水平半径OA高H处自由落下，沿竖直平面内的轨道通过D点时对轨道的压力等于其重力的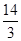
倍，试求：
⑴高度H的大小；
⑵讨论此球能否到达BDO轨道的O点，并说明理由；
⑶小球沿轨道运动后再次落到轨道上的速度的大小和方向。
答案
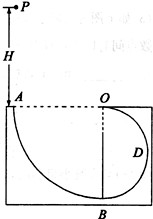
⑴H＝10m；⑵能到达O点；⑶v＝17.3m/s，方向与水平方向成夹角θ＝arctan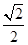
题目分析：⑴设小球通过D点时的速度为vD，此时轨道对小球的弹力提供了小球做圆周运动的向心力，根据牛顿第二定律有：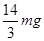
＝
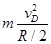①
小球从P点运动至D点的过程中，根据动能定理有：mg(H＋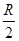
)＝
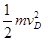－0 ②
由①②式联立解得：H＝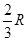
＝10m ③
⑵设小球能沿圆轨道运动至O点，速度为v0，根据动能定理有：mgH＝
－0 ④
由③④式联立解得：v0＝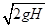
＝
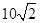m/s ⑤
假设小球恰好通过圆轨道最高点O的速度为vC，根据牛顿第二定律有：mg＝
解得：vC＝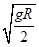
＝
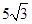m/s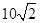＜m/s，所以，小球能够到达BDO轨道的O点
⑶小球通过O点后做平抛运动，设经过时间t落到AB圆弧轨道上，根据平抛运动规律可知，小球在水平方向通过的位移为：x＝v0t ⑥
在竖直方向通过的位移为：y＝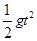
⑦
显然x、y满足圆轨迹方程：x2＋y2＝R2 ⑧
由⑤⑥⑦⑧式联立，并代入数据解得：t＝1s
所以小球再次落到轨道上的速度大小为：v＝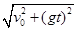
＝
m/s＝17.3m/s
方向与水平方向间的夹角为：θ＝arctan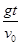
＝arctan