问题
计算题
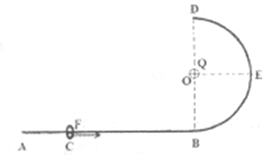
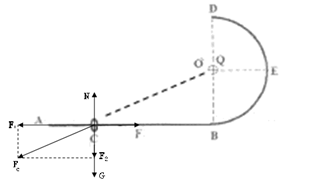
（10分）一端弯曲的光滑绝缘杆ABD固定在竖直平面上，如图所示，AB段水平，BD段是半径为R的半圆弧，有一电荷量为Q的正点电荷固定在圆心O点。一质量为m、电荷量为q的带正电小环套在光滑绝缘杆上，在大小为F的水平恒力作用下从C点由静止开始运动，到B点时撤去恒力，小环继续运动到达D点，已知CB间距为4R/3。（提示：根据电磁学有关知识，在某一空间放一电荷量为Q的正点电荷，则距离点电荷为r的某点的电势为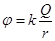
，其中k为静电力常量，设无穷远处电势为零）。
（1）定性说明从C运动到D过程小环的电势能如何变化
（2）小环在C点时加速度为多大
（3）求水平恒力F的最小值。
答案
（1）从C运动到B过程电势能增大；从B运动到D过程电势能不变。
（2）
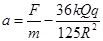
（3）
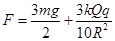
题目分析：（1）从C运动到B过程电场力对小环做负功，电势能增大； （1分）
从B运动到D过程电场力不做功，电势能不变。 （1分）
（2）对小环受力分析如图，由牛顿第二定律，小环在C点时加速度a满足
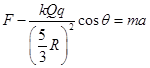（3分）
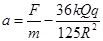（1分）
（3）小环刚好运动到达D点，
水平恒力F的最小
C、D两点的电势差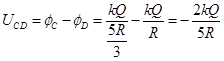
（1分）
从C运动到D过程中由动能定理
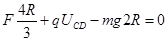（2分）
解得水平恒力F的最小值 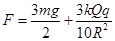（1分）
