问题
选择题
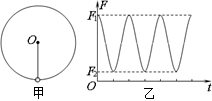
一宇航员到达半径为R、密度均匀的某星球表面，做如下实验：用不可伸长的轻绳拴一质量为m的小球，上端固定在O点，如图甲所示，现在最低点处给小球一初速度，使其绕O点在竖直平面内做圆周运动，通过传感器记录下绳中拉力大小F随时间t的变化规律如图乙所示，已知F1的大小等于7F2，引力常量为G，各种阻力不计，则( )
A．该星球表面的重力加速度为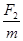
B．卫星绕该星球的第一宇宙速度为
C．该星球的质量为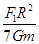
D．小球通过最高点的最小速度为零
答案
AC
题目分析：根据图象可知，小球在最低点时，绳的拉力为F1，设此时小球的速度为v1，绳长为r，星球的重力加速度为g，根据牛顿第二定律有：F1－mg＝
，同理在最高点时有：F2＋mg＝
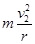，在由最低点运动至最高点的过程中，根据动能定理有：－2mgr＝
－
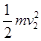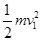，联立以上三式解得：g＝
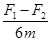，又因为F1＝7F2，所以g＝
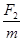，故选项A正确；设卫星绕该星球的第一宇宙速度为v，该星球的质量为M，根据万有引力定律和牛顿第二定律有：
＝
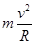，解得：v＝
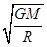，故选项B错误；在星球表面处有：＝mg，解得：M＝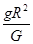
＝
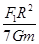，故选项C正确；小球通过最高点时，根据牛顿第二定律有：F2＋mg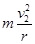＝≥mg，所以v2≥
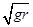，即小球通过最高点的最小速度为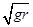，故选项D错误。