问题
计算题
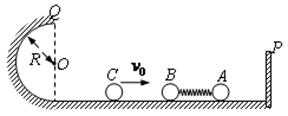
(17分)可视为质点的小球A、B静止在光滑水平轨道上,A的左边固定有轻质弹簧,B与弹簧左端接触但不拴接,A的右边有一垂直于水平轨道的固定挡板P。左边有一小球C沿轨道以某一初速度射向B球,如图所示,C与B发生碰撞并立即结成一整体D,在它们继续向右运动的过程中,当 D和A的速度刚好相等时,小球A恰好与挡板P发生碰撞,碰后A立即静止并与挡板P粘连。之后D被弹簧向左弹出,D冲上左侧与水平轨道相切的竖直半圆光滑轨道,其半径为 ,D到达最高点Q时,D与轨道间弹力
,D到达最高点Q时,D与轨道间弹力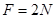 。已知三小球的质量分别为
。已知三小球的质量分别为 、
、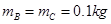 。取
。取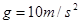 ,求:
,求:
(1)D到达最高点Q时的速度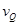 的大小;
的大小;
(2)D由Q点水平飞出后的落地点与Q点的水平距离s;
(3)C球的初速度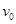 的大小。
的大小。
答案
(1)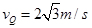 (2)
(2) (3)
(3)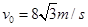
题目分析: ⑴D在Q点时据牛顿第二定律有: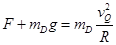
解得: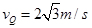
⑵令D由Q点平抛飞出后经时间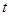 落至地面
落至地面
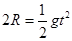
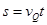
代入数据解得:
⑶C碰B,据动量守恒有: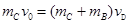
解得: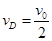
D向右压缩弹簧的过程中,据系统动量守恒: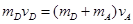
解得: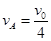
据机械能守恒: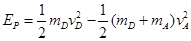
解得: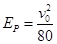
A碰P静止后,D被弹簧向左弹出直到Q的过程中,据机械能守恒有: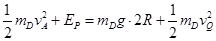
代入数据解得: