问题
计算题
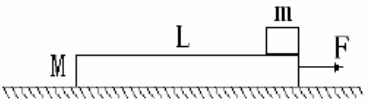
如图所示, 木板静止于水平地面上, 在其最右端放一可视为质点的木块. 已知木块的质量m＝1 kg, 木板的质量M＝4 kg, 长L＝2.5 m, 上表面光滑, 下表面与地面之间的动摩擦因数μ＝0.2.现用水平恒力F＝20 N拉木板, g取10 m/s2, 求:
（1）要使木块能滑离木板, 水平恒力F作用的最短时间;
（2）如果其他条件不变, 假设木板的上表面也粗糙, 其上表面与木块之间的动摩擦因数为μ1＝0.3, 欲使木板能从木块的下方抽出, 需对木板施加的最小水平拉力；
答案
（1）t=1s；（2） F＞25N
题目分析:（1）木板受到的摩擦力：f=μ（M+m）g=10N．
由牛顿第二定律，木板的加速度：a＝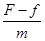
=2.5m/s2
设作用t时间后撤去力F，由牛顿第二定律，木板的加速度为a′=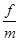
=-2.5m/s2
木板先做匀加速运动，后做匀减速运动，且a=-a′，故at2=L．
得：t=1s．
（2）设木块的最大加速度为a1，木块的最大加速度为a2，则
对木块：f1=μ1mg=ma1．
对木板：F1-f1-μ（M+m）g=Ma2
木板从木块的下方抽出的条件：a1> a2
解得：F1＞25N