问题
问答题
在图中，一个封闭的盒子内有两块隔板， 把盒子隔成了三个容器，每个容器内有2 个球，球上各有一个字，每个容器中球上的字恰好组成一个词（从左向右念）．摇动盒子，球在容器内的左右位置可以变换．
(1) 图中6 个球同时排列成三个词的概率是多少？
(2)取去其中一块隔板，摇动盒子，6个球能同时排列成三个词的概率又是多少？
(3)把两块隔板全部取去，摇动盒子，6个球能同时排列成 三个词的概率又是多少？
(4)在这个封闭的系统（盒子）内，取消隔板让小球在系统内自发、充分地运动，其无序性是增大了还是减小了？
答案
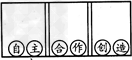
解：(1)图中6个球总共有8种不同的排列，所以同时排列成三个词的概率为
(2)若取去右边的隔板，右边4个球能组成“合作、创造”“创造、合作”“合造、创作”“创作、合造”共4种排列，而总共的排列数为
种，所以此时能排列成三个词的概率为
若取去左边的隔板，左边4个球能组成“自主、合作”“合作、自主”共2种排列，而总共的排列数为48种，此时的概率为
(3)若将两块隔板同时取去，6个球能分别组成三个词，分别为“自主、合作、创造”“自主、合造、创作”“自创、合造、作主”“自造、合作、主创”，每组的排列数为6种，而6个球总共的排列数为
种= 720种，所以6个球能同时排列成三个词的概率为
(4)取消隔板后让小球在系统内自发、充分地运动，其无序性增大了，即熵增加了．