某汽车制造厂开发了一款新式电动汽车,计划一年生产安装240辆.由于抽调不出足够的熟练工来完成新式电动汽车的安装,工厂决定招聘一些新工人;他们经过培训后上岗,也能独立进行电动汽车的安装.生产开始后,调研部门发现:1名熟练工和2名新工人每月可安装8辆电动汽车;2名熟练工和3名新工人每月可安装14辆电动汽车.
(1)每名熟练工和新工人每月分别可以安装多少辆电动汽车?
(2)如果工厂招聘n(0<n<10)名新工人,使得招聘的新工人和抽调的熟练工刚好能完成一年的安装任务,那么工厂有哪几种新工人的招聘方案?
(3)在(2)的条件下,工厂给安装电动汽车的每名熟练工每月发2000元的工资,给每名新工人每月发1200元的工资,那么工厂应招聘多少名新工人,使新工人的数量多于熟练工,同时工厂每月支出的工资总额W(元)尽可能的少?
(1)设每名熟练工和新工人每月分别可以安装x,y辆电动汽车.
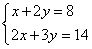 解得
解得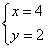
答:每名熟练工和新工人每月分别可以安装4辆、2辆电动汽车;
(2)设需熟练工m名,依题意有:2 n×12+4m×12=240, n =10-2m
∵0<n<10 ∴0<m<5 故有四种方案:(n为新工人)
∴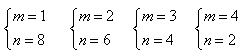 ;
;
(3)依题意有:W=1200n+(5-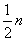 )×2000=200 n+10000,
)×2000=200 n+10000,
要使新工人数量多于熟练工,满足n=4、6、8,
故当n=4时,W有最小值=10800元
