（1）在《探究加速度与力、质量的关系》实验中
①某小组同学用如图所示装置，采用控制变量方法，研究在小车质量不变的情况下，小车加速度与小车受力的关系。下列说法正确的是
A．平衡摩擦力的方法就是将木板一端垫高，在塑料小桶中添加砝码，使小车在绳的拉力作用下能匀速滑动
B．每次改变小车所受的拉力时，不需要重新平衡摩擦力
C．实验中应先放小车，然后再开打点计时器的电源
D．在每次实验中，应使小车和砝码的质量远大于砂和小桶的总质量
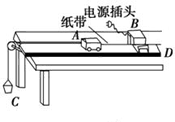
②如图所示是某一次打点计时器打出的一条记录小车运动的纸带．取计数点A、B、C、D、E、F、G．纸带上两相邻计数点的时间间隔为T = 0.10s，用刻度尺测量出各相邻计数点间的距离分别为AB=1.50cm，BC="3.88" cm，CD="6.26" cm，DE="8.67" cm，EF="11.08" cm，FG=13.49cm，则小车运动的加速度大小a = _____ m/s2，打纸带上C点时小车的瞬时速度大小VC = ______ m/s．（结果保留二位有效数字）
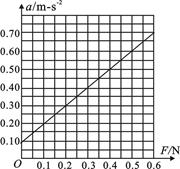
③某同学测得小车的加速度a和拉力F的数据如下表所示（小车质量保持不变）：
| F/N | 0.20 | 0.30 | 0.40 | 0.50 | 0.60 |
| a/ m/s2 | 0.30 | 0.40 | 0.48 | 0.60 | 0.72 |
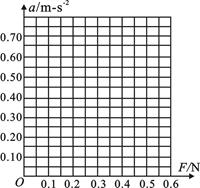
b．若作出的a-F图象不过坐标原点，可能的原因是：_______________________。
（2）在测定一节干电池的电动势和内电阻的实验中，
实验室备有下列器材选用：
干电池（电动势E约为1.5V，内电阻r约为1.0Ω）；电流表G（满偏电流2.0mA，内阻Rg=10Ω）；
电流表A（量程0~0.6A，内阻约为0.5Ω）；
滑动变阻器R1（0~20Ω，10A）；
滑动变阻器R2（0~300Ω,1A）；
定值电阻R0=999Ω；
开关和导线若干。
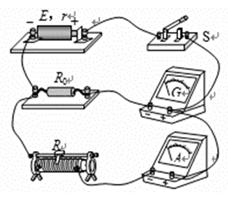
某同学设计了如图甲所示的电路进行实验：
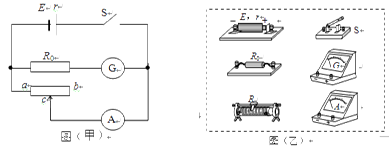
①该电路中为了操作方便且能准确地进行测量， 滑动变阻器应选 （填写器材前的字母代号“R1”或“R2”）； 在闭合开关S前，应将滑动变阻器的滑动端c移动至
（填“a端”、“中央”或“b端”）。
②根据图甲在图乙的实物图上连线。
（1）①BD ② 2.4 ；0.50或0.51 ③ a.如图
b平衡摩擦过度或木板一端垫得过高
（2）、①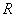
， b端 ②如图
题目分析：（1）①A、实验时首先要平衡摩擦力，平衡摩擦力的方法就是，小车与纸带相连，小车前面不挂小桶，把小车放在斜面上给小车一个初速度，看小车能否做匀速直线运动，故A错误；
B、平衡摩擦力时，是重力沿木板方向的分力等于摩擦力，即：mgsinθ=μmgcosθ，可以约掉m，只需要平衡一次摩擦力，每次改变拉小车的拉力后都不需要重新平衡摩擦力，故B正确；
C、为了提高纸带的利用率，在纸带上尽量多的打点，因此实验中应先接通电源，后放开小车，故C误；
D、每次实验中，应使小车和砝码的质量远大于砂和小桶的总质量，故D正确；
故选：BD
②根据匀变速直线运动的推论公式△x=aT2可得：
设A到B之间的距离为x1，以后各段分别为x2、x3、x4、x5、x6，
根据匀变速直线运动的推论公式△x=aT2可以求出加速度的大小，得：
x4-x1=3a1T2
x5-x2=3a2T2
x6-x3=3a3T2
为了更加准确的求解加速度，我们对三个加速度取平均值，得：
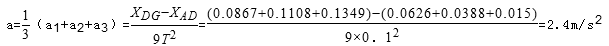
根据匀变速直线运动中时间中点的速度等于该过程中的平均速度，可以求出打纸带上C点时小车的瞬时速度大小．
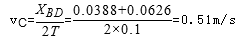
③根据表中的数据在坐标图上运用描点法作出a-F图象
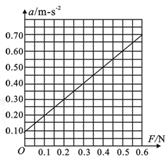
由图象可知，a-F图象在a轴上有截距，这是由于平衡摩擦力过度或木板一端垫得过高造成的．
（2）①测量电动势和内电阻需要有电压表和电流表；但题目中只给出两个电流表；但其中一个电流表G的内阻已知，可以把内阻已知的电流表和定值电阻串联改装成一个电压表．同时因电流表量程较大，故为了减少误差，滑动变阻器需选小电阻，故选R；为保证安全，开始时滑动变阻器应接到最大值，故应接b端；
②由原理图可知，电路为基本的限流接法，故按原理图串联即可；连线如图乙所示：
