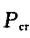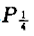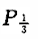如图所示，两根足够长、电阻不计、间距为d的光滑平行金属导轨，其所在平面与水平面的夹角为θ，导轨平面内的矩形区域abcd内存在有界匀强磁场，磁感应强度大小为B，方向垂直于导轨平面向上，ab与cd之间相距为L，金属杆甲、乙的阻值相同，质量均为m，甲杆在磁场区域的上边界ab处，乙杆在甲杆上方与甲相距L处，甲、乙两杆都与导轨垂直．静止释放两杆的同时，在甲杆上施加一个垂直于杆平行于导轨的外力F，使甲杆在有磁场的矩形区域内向下做匀加速直线运动，加速度大小为a＝2gsin θ，甲离开磁场时撤去F，乙杆进入磁场后恰好做匀速运动，然后离开磁场．
(1)求每根金属杆的电阻R.
(2)从释放金属杆开始计时，求外力F随时间t变化的关系式，并说明F的方向．
(3)若整个过程中，乙金属杆 * * 生热量Q，求外力F对甲金属杆做的功W.
(1)
(2)mgsin θ＋mgsin θ·
t(0≤t≤
)，方向垂直于杆且平行于导轨向下
(3)W＝2Q
(1)设甲在磁场区域abcd内运动的时间为t1，乙从释放到运动至ab位置的时间为t2，则L＝
·2gsin θ·t
，
L＝gsin θ·t
所以t1＝，t2＝
因t1＜t2，所以甲离开磁场时，乙还没有进入磁场
设乙进入磁场时的速度为v1，乙中的感应电动势为E1，回路中的电流为I1，则有
mv＝mgLsin θ，E1＝Bdv1，I1＝
，mgsin θ＝BI1d
联立解得R＝.
(2)从释放金属杆开始计时，设经过时间t，甲的速度为v，甲中的感应电动势为E，回路中的电流为I，则v＝at，E＝Bdv，I＝
，F＋mgsin θ－BId＝ma
联立解得F＝mgsin θ＋mgsin θ·t(0≤t≤)
方向垂直于杆且平行于导轨向下．
(3)甲在磁场中运动过程中，乙没有进入磁场，设甲离开磁场时速度为v0，甲、乙产生的热量相同，设为Q1，则v
＝2aL
由功能关系知W＋mgLsin θ＝2Q1＋mv
解得W＝2Q1＋mgLsin θ
乙在磁场中运动过程中，甲、乙产生相同的热量，设为Q2，则2Q2＝mgLsin θ
根据题意有Q＝Q1＋Q2
联立解得W＝2Q.
