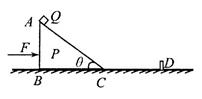
如图所示,水平地面上有一个静止的直角三角滑块P,顶点A到地面的距离h=1.8m,水平地面上D处有一固定障碍物,滑块的C端到D的距离L=6.4m。在其顶点么处放一个小物块Q,不粘连,最初系统静止不动。现在滑块左端施加水平向右的推力F=35N,使二者相对静止一起向右运动,当C端撞到障碍物时立即撤去力F,且滑块P立即以原速率反弹,小物块Q最终落在地面上。滑块P的质量M=4.0kg,小物块Q的质量m=1.0kg,P与地面间的动摩擦因数 。(取g=10m/s2)求:
。(取g=10m/s2)求:
(1)小物块Q落地前瞬间的速度;
(2)小物块Q落地时到滑块P的B端的距离。
(1)Q落地前瞬间的速度大小为vt=10m/s 与水平成37°角 (2)9.24m
题目分析:(1)对P、Q整体分析有:F-μ(m+M)g=(m+M)a1 (1分)
a1=5m/s2 (1分)
当顶点C运动至障碍物D时有:vD2=2a1L (1分)
vD =8m/s (1分)
之后Q物体做平抛运动有:h=gt12/2 (1分)
t1=0.6s (1分)
Q落地前瞬间竖直方向的速度为vy=gt1 (1分)
vy=6m/s (1分)
由矢量合成得:Q落地前瞬间的速度大小为vt="10m/s" (1分)
与水平成φ角,tanφ=vy / vD φ=37° (1分)
(2)由(1)得Q平抛的水平位移x1=vDt1 (1分)
x1=4.8m (1分)
P物体做匀减速运动,μMg=Ma2 (1分)
a2=2m/s2 vD = a2t2 (1分)
t2=4s>t1 (1分)
Q物体平抛时间内P的位移为x2=vDt1-a2t12/2 (1分)
x2=4.44m (1分)
所以Q落地时Q到滑块B端的距离为x=x1+x2 =9.24m (1分)
