问题
单项选择题
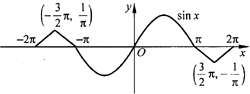
如下图所示，连续函数y=f(x)在[-π,π)上的图形是sinx的图形，在[-2π,-π)和 [π,2π]上的图形是底边长为π，高为
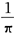的等腰三角形的两腰，设
，则下列结论正确的是( )．
答案
参考答案：C
解析：[*]
由定积分的几何意义，F(2π)等于曲线g(x)=sinx与x轴(0≤x≤π)所围面积减去等腰三角形面积，即[*]
[*]
又从f(x)的图形可知，f(x)在[-2π,2π]上是奇函数，因此，[*]是偶函数，所以F(2π)=F(-2π)F(π)=F(-π)，从而F(2π)= [*]．故正确选项为C．
