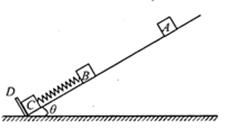
如图所示,质量均为m的物体B、C分别与轻质弹簧的两端相栓接,将它们放在倾角为θ的足够长的光滑斜面上,静止时弹簧的形变量为x0。斜面底端有固定挡板D,物体C靠在挡板D上。将质量也为m的物体A从斜面上的某点卣静止释放,A与B相碰。已知重力加速度为g,弹簧始终处于弹性限度内,不计空气阻力。
(1)若A与B相碰后粘连在一起做简谐运动,求AB通过平衡位置时弹簧的形变量;
(2)在(1)问中,当AB第一次振动到最高点时,C对挡板D的压力恰好为零,求振动过程C 对挡板D的压力最大值:
(3)若将A从距离B为9x0。的位置由静止释放,A与B相碰后不粘连,但仍立即一起运动,且当B第一次运动到最高点时,C对挡板D的压力也恰好为零。已知A与B相碰后,A、B系统动能损失一半,求A与B相碰后弹簧第一次恢复到原长时B的速度大小。
(1) (2)
(2)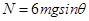 (3)
(3)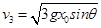
题目分析::(1)碰撞前,由平衡条件得:对B: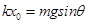 ①,
①,
碰撞后经过平衡位置时,对AB组成的系统,
由平衡条件得: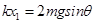 ②,
②,
由①②解得: ;
;
(2)物体C对D挡板的压力为0时,设AB加速度为a,
对C,弹簧的弹力: ③
③
对AB,由牛顿第二定律得: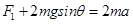 ④
④
物体C对挡板D的压力N最大时,根据对称性可知,AB的加速度大小仍为a,
设此时弹簧秤的弹力为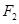 ,
,
对AB,由牛顿第二定律得: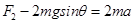 ⑤
⑤
对C: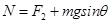 ⑥
⑥
由③④⑤⑥解得: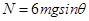 ,
,
由牛顿第三定律可知,C对挡板D压力的最大值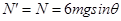 ;
;
(3)A从开始下滑到与B碰撞前过程中,
由机械能守恒定律得: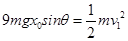 ,
,
AB碰撞动能损失一半,碰撞后,
AB系统: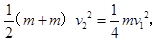
设弹簧形变量为x0弹性势能为EP,从AB开始压缩弹簧到弹簧第一次恢复原长时,
AB的速度为v3,由机械能守恒定律得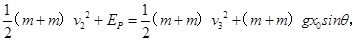
当弹簧第一次恢复原长时,A、B恰好分离,从A、B分离到B运动到最高点过程中,
由机械能守恒定律得: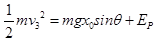 ,
,
解得A、B碰撞后弹簧第一次恢复原长时,B的速度大小为: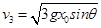 ;
;
