问题
计算题
(10分)如图所示,在竖直面内有两平行金属导轨AB、CD.导轨间距为L,电阻不计.一根电阻不计的金属棒ab可在导轨上无摩擦地滑动.棒与导轨垂直,并接触良好.导轨之间有垂直纸面向外的匀强磁场,磁感强度为B.导轨右边与电路连接.电路中的三个定值电阻阻值分别为2R、R和R.在BD间接有一水平放置的电容为C的平行板电容器,板间距离为d.
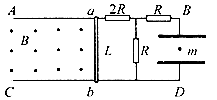
(1)当ab以速度v0匀速向左运动时,电容器中质量为m的带电微粒恰好静止.试判断微粒的带电性质和电容器的电量q
(2)ab棒由静止开始,以恒定的加速度a向左运动.讨论电容器中带电微粒的加速度如何变化.(设带电微粒始终未与极板接触.)
答案
(1)负电;CBLv0/3;(2)见解析;
题目分析:ab棒匀速向左运动时,棒中产生的感应电流方向为a→b,则电容器上板带正电,下板带负电,场强方向向下.∵微粒受力平衡,电场力方向向上,∴微粒带负电。
UC=E/3=BLv0/3,q=CUC=CBLv0/3
(2)设经过时间t0,微粒受力平衡,则 mg=qUC/d;UC=E/3=BLat/3;
解得,t=3mgd/(BLaq)
当t<t0时,根据牛顿第二定律得:a1=g-BLaqt/(3md),越来越小,加速度方向向下;
当t=t0时,a2=0;
当t>t0时,根据牛顿第二定律得:a3= BLaqt/(3md)-g,越来越大,加速度方向向上;
