问题
问答题
设函数f(x)满足f(1)=1，且对x≥1，有f’(x)=
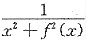，试证极限
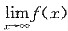存在，且极限值小于
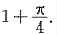
答案
参考答案：[证] 因为f’(x)处处为正，所以f(x)严格单增，从而当t＞1时，有f(t)＞1，
所以
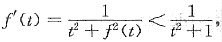
于是
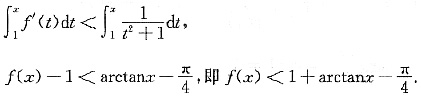
由于f(x)递增且有界，所以
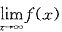存在，且至多为
搜题请搜索小程序“爱下问搜题”
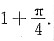
设函数f(x)满足f(1)=1，且对x≥1，有f’(x)=
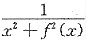，试证极限
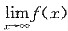存在，且极限值小于
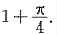
参考答案：[证] 因为f’(x)处处为正，所以f(x)严格单增，从而当t＞1时，有f(t)＞1，
所以
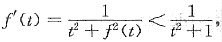
于是
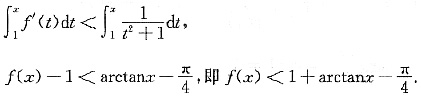
由于f(x)递增且有界，所以
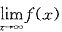存在，且至多为
