问题
问答题
设曲线方程为y=e-x(x≥0).
(Ⅰ)把曲线y=e-x,x轴,y轴和直线x=ξ(ξ>0)所围平面图形绕x轴旋转一周,得一旋转体,求此旋转体的体积V(ξ),并求满足V(a)=
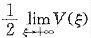 的a;
的a;
(Ⅱ)在此曲线上找一点,使过该点的切线与两个坐标轴所夹平面图形的面积最大,并求出该面积.
答案
参考答案:
解析: (Ⅰ)V(ξ)=
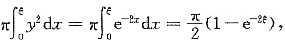
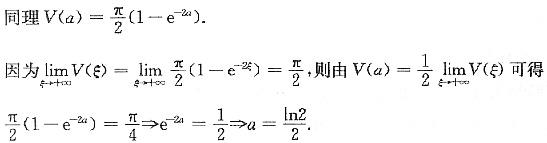
(Ⅱ)设切点为(x0,e-x0),则切线方程为y-ee-x0=-e-x0(x-x0).
写成截距式方程为
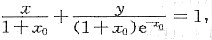
所以,切线与两坐标轴所围面积为

所以S在x0>0内只有一个驻点x0=1,又问题本身的确存在最大值,
所以x0=1即为最大值点,因而切点为(1,e-1),最大面积为S=2e-1.
